Pair correlation functions with free-form boundaries for distribution inpainting and decomposition

Baptiste Nicolet1 Pierre Ecormier-Nocca1 Pooran Memari1 Marie-Paule Cani1
1École Polytechnique, CNRS (LIX), IP Paris

In Eurographics, 2020

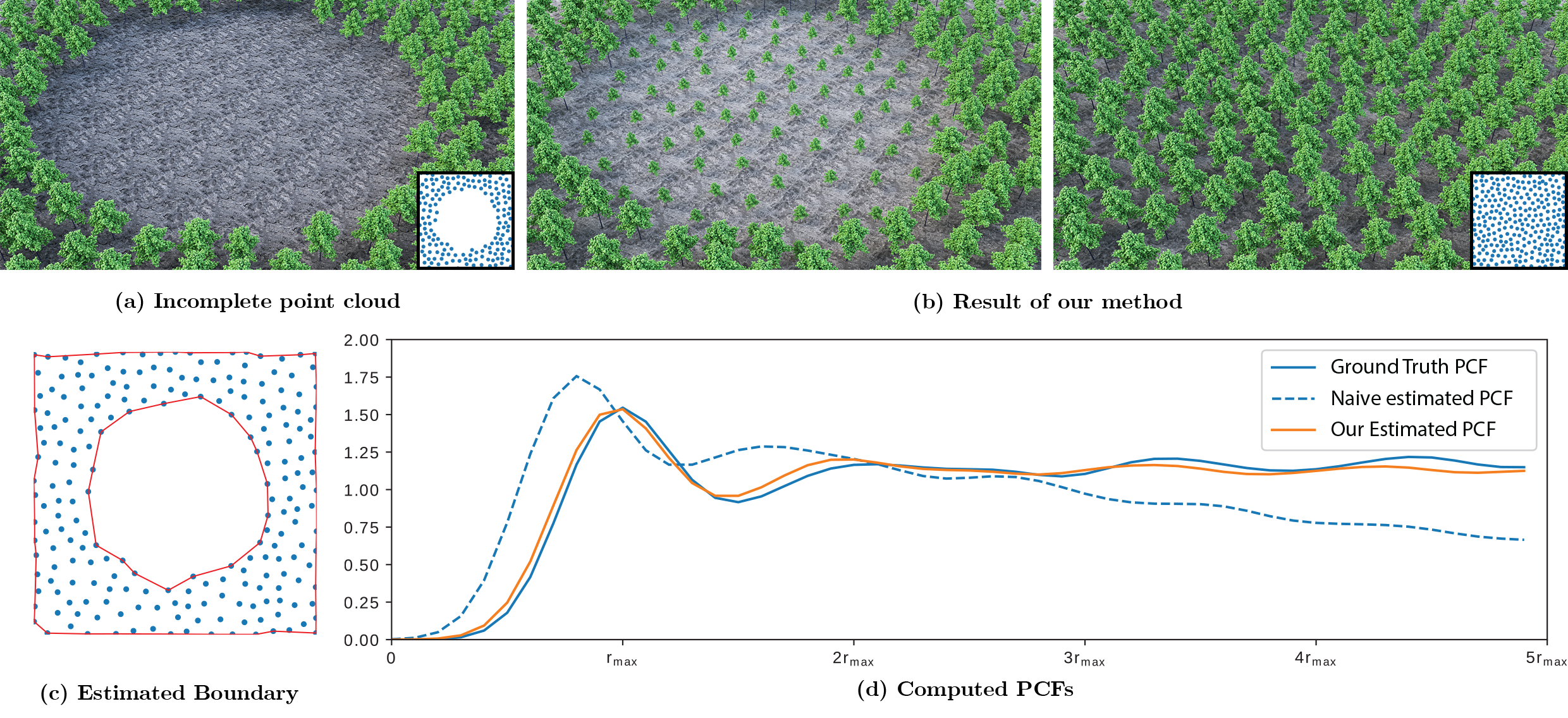
Teaser
Application of extended PCFs to the inpainting of distributions, illustrated by the re-planting of a partially destroyed forest (a,b).From an incomplete dataset (a), our method accurately estimates free-form boundaries (c) and compensates from missing points when learning PCFs (d). This allows us to restore the perceived initial distribution at the synthesis stage (b)

Abstract

Pair Correlation Functions (PCF) have been recently spreading as a reliable representation for distributions, enabling the efficient synthesis of point-sets, vector textures and object placement from examples. In this work we introduce a triangulationbased local filtering method to extend PCF-based analysis to exemplars with free-form boundaries. This makes PCF applicable to new problems such as the inpainting of missing parts in an input distribution, or the decomposition of complex, non-homogeneous distributions into a set of coherent classes, in which each category of points can be studied together with their intra and inter-class correlations.

Downloads

Reference

Baptiste Nicolet, Pierre Ecormier-Nocca, Pooran Memari, Marie-Paule Cani. Pair correlation functions with free-form boundaries for distribution inpainting and decomposition. Eurographics, 2020. 
@inproceedings{nicolet2020pair,
    author = "Nicolet, Baptiste and Ecormier-Nocca, Pierre and Memari, Pooran and Cani, Marie-Paule",
    title = "Pair Correlation Functions with Free-Form Boundaries for Distribution Inpainting and Decomposition",
    booktitle = "Eurographics",
    year = "2020"
}